Pushing 3D Diffusion-Limited Aggregation even further

Posted by softologyblog on May 22, 2017

If you don’t know what Diffusion-Limited Aggregation (aka DLA) is, see this post of mine.

Previous Results

Previously, my best 3D DLA movies were these two;

I had two main issues with those movies. Firstly, I used software based OpenGL which does not support shadows or any advanced lighting techniques. Secondly, I was launching the moving particles on the surface of a sphere that was biased to the poles, which meant the resulting growth tended to grow more in the “up” and “down” directions rather than a nice spherical shape. This is especially noticable in the first movie above that grows more in the up direction than the other directions.

64-bit

Now that Visions of Chaos is 64-bit I wanted to push the limits of the DLA animations even further. In the past the 32-bit executable limited me to around 3GB of usable memory which restricted the size of the arrays that I could grow DLA structures within to around 750x750x750. With a 64-bit executable Visions of Chaos can now use as much memory as the PC has available.

Bugs in old code

I have been experimenting with 2D and 3D DLA for many years now and my existing code reflected that. When I started expanding the grid size and particle counts I was getting strange crashes/hangs/poor behavior. As any programmer knows, you think “this will be an easy fix”. Well, 3 or 4 days later after trying to fix these simple bugs and rendering lengthy test runs I was ready to chuck my PC out the window. Having to wait a few hours to see if a fix works or not really tests the patience. In the end I bit the bullet and woke up one morning and rewrote the code from scratch. It took a few hours and I now have a much more stable and faster version. I also added support for Mitsuba so I get nicely shaded images. Back on track.

Latest results

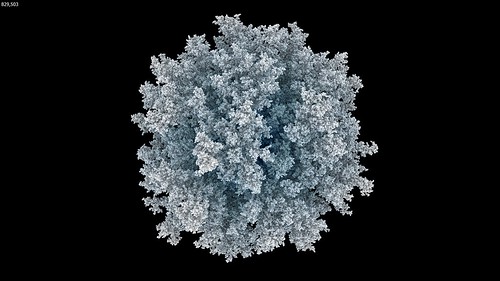
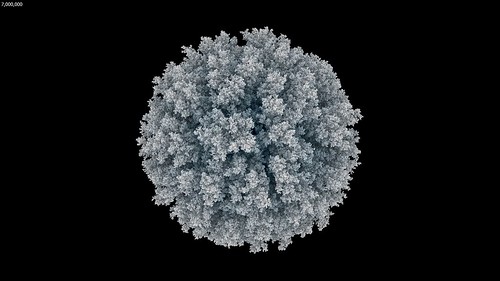
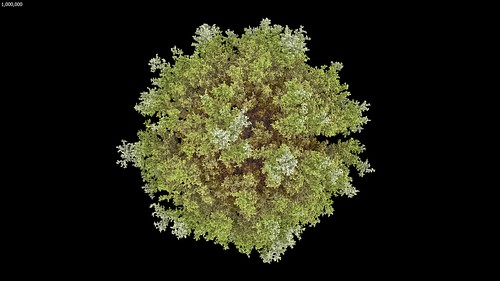
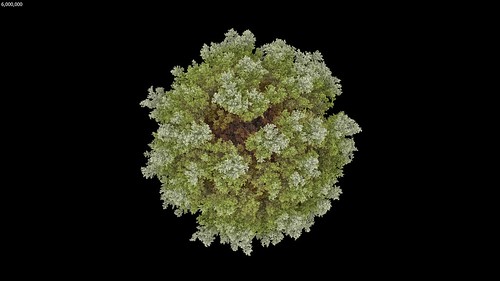
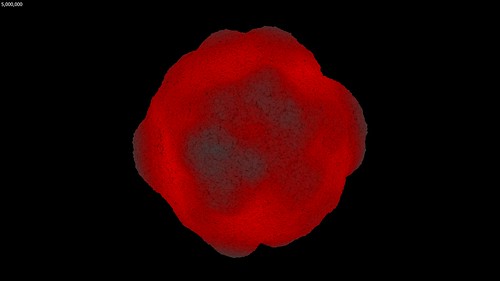
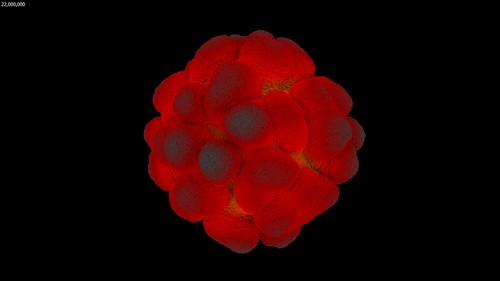
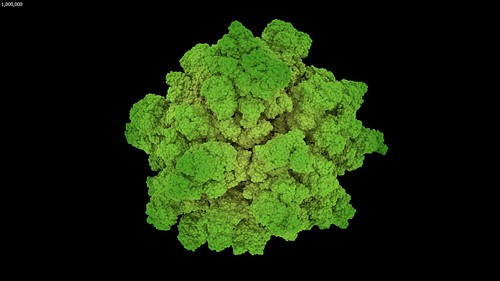
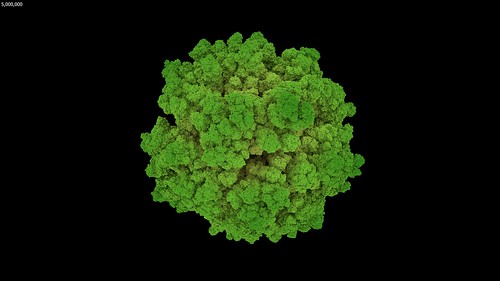
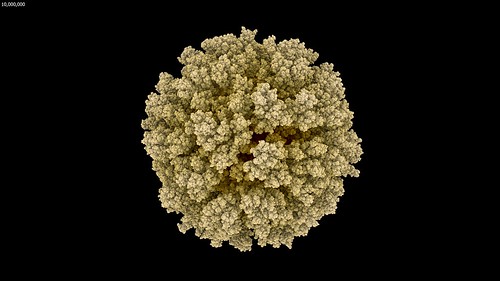
With the extra memory available from a 64-bit Visions of Chaos executable and being able to use Mitsuba to render each frame it was time to let my PC churn away for a few days rendering DLA frames. The few days expanded into a few weeks as I kept tweaking settings and code and started to render the DLA movie parts again from scratch. But finally, the following movie was complete.

I only have 32 GB memory in my main PC so those sample movies run out of RAM when around 10 million particles are reached. This is double the maximum particles I achieved in the past. I need to look at maxing out my memory to 128 GB so I can create even larger DLA structures.

Something to observe in that movie is how once the particle count gets beyond around one million the overall structure remains the same as it continues to grow. This is a great example of the self-similarity properties of fractals. With more memory and more particles the overall structure would not suddenly change beyond 10 million particles. The individual spheres would shrink into sub pixel sizes, but the overall growing shapes would remain self-similar (as render times continued to increased per frame). This is also noticeable in most of the sample images in this post.

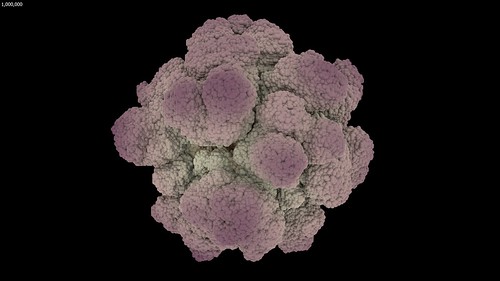
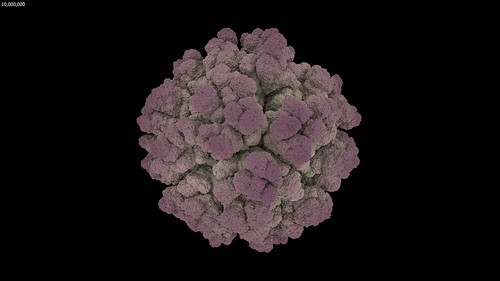
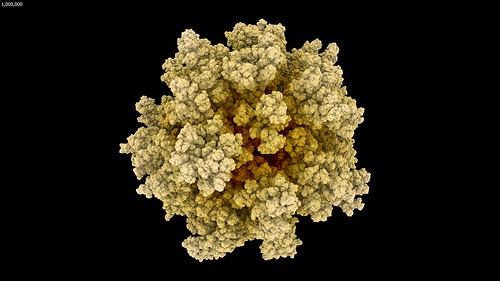
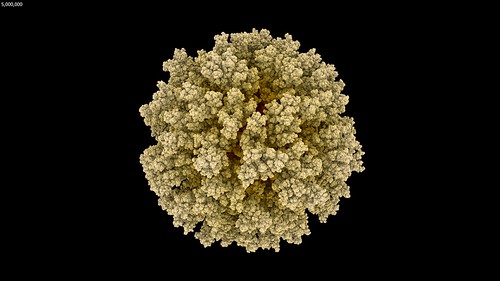
RenderMan Blobby Implicit Surfaces

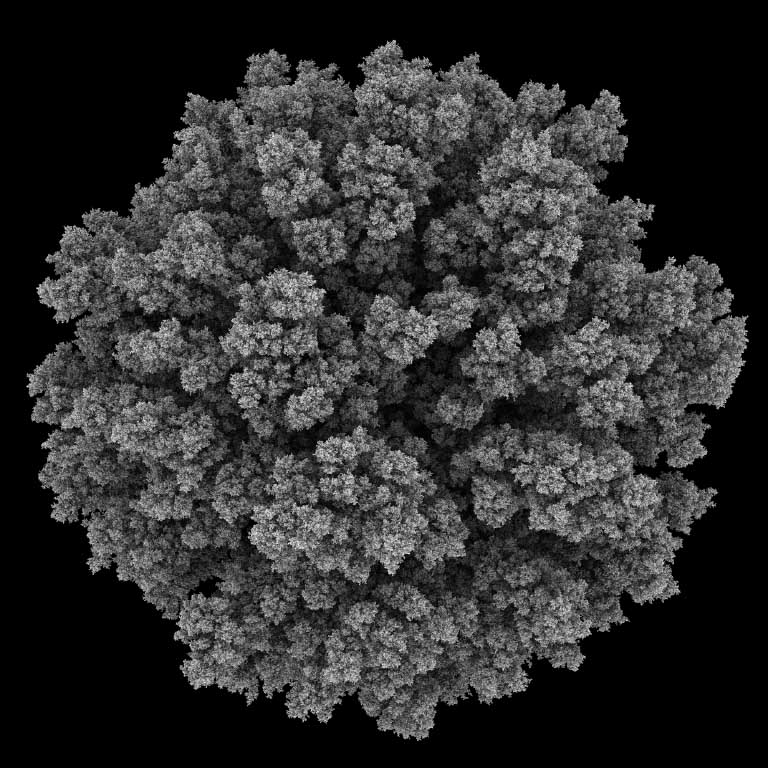
Using RenderMan as a rendering engine allows the use of blobby implicit surfaces aka metaballs. The metaball process merges the individual spheres into a blobby surface and gives the following result.

I didn’t let these examples run for as long as the previous example movie. This is because they were mainly as a quick example of blobby implicit surface rendering. Also because they were reaching the levels of detail that further steps don’t add any new structure shapes (due to the self similarity of DLA). And mainly because RenderMan was starting to stretch my patience taking over 6 minutes to render each frame.

Some DLA coding tips for programmers

If you are not programming 3D DLA then this next bit will be of little use to you and you can feel free to skip it.

When launching particles into the DLA space use random points on a sphere surrounding the current growth. If you use random points on a cube surrounding the growth it will be biased to grow along the axiis. Using a sphere helps maintain a more spherical growth. Set the radius of the sphere slightly larger than the furthest distance the dla structure has grown. ie if the furthest particle is 10 units of length from the origin, then set the sphere size to 13. Also make sure you use an even distribution of points on the sphere surface. My original code was biased to the poles and this is why the first sample movie above grows towards the up/north direction more than evenly in all directions. Some quick code to evenly distribute random points on a sphere is


theta:=2*pi*random;
phi:=arccos(1-2*random);
px:=round(sin(phi)*cos(theta)*launchradius)+centerx;
py:=round(sin(phi)*sin(theta)*launchradius)+centery;
pz:=round(cos(phi)*launchradius)+centerz;

The usual DLA method is to wait until a moving particle goes “off screen” before a new particle is launched. For 3D, off screen is the array dimensions. Waiting for particles to move off the existing DLA grid can really slow down the process (especially for large sized grids). Rather than wait for the edge of the grid, use a few grid units distance beyond the launch sphere radius. So if the launch sphere is radius 13 then moving particles get discarded if they travel more than 16 distance from the origin.

Calculating distances involves costly sqrt calculations. If you are doing a sqrt each time the particle is moving they quickly add up and slow down the simulation. To speed up distance calcs I fill an array once at the start of the simulation that contains the distance from the origin (grid center) to each array location. This makes it much quicker when you want to know how far a moving particle is from the origin. All it takes is a single array lookup rather than a sqrt distance calculation.

Another thing you want to know for moving particles is how many neighbor particles is it touching. For example if the current settings make a particle stick to 3 or more existing neighbors then you usually do a quick loop of neighbor cells adding them up. Again, doing this every time the moving particles move adds up and slows everything down. I use another array that holds the neighbor count for each grid location. When a new particle attaches to the existing DLA structure, you add 1 to the surrounding cells in the neighbors array. Much faster.

If you are rendering a very dense DLA then there will be a lot of particles within the middle that remain hidden. Doing a quick check to see if a particle is surrounded (ie using the above neighbors array means if neighbors=26) means it can be skipped and not sent to Mitsuba for rendering. On the densest DLA structures this cut down the number of spheres passed to OpenGL and/or Mitsuba to only 7% of the total spheres. A huge speed up in terms of time per frame.

You need to auto-increase the hits per update each frame. ie if you set the display to update every time 10 particles get stuck to the growing structure it will look fine at the start, but once the structure starts growing you will have a long wait to get to a million particles and beyond. I used a simple formula of increasing the stuck particles per frame as the number of total stuck particles div 40. Once you get to 100000 particles, keep the update at 25,000 particles per frame. This allows a nice smooth increase in stuck particles and gets you to the more interesting million+ range quicker.

Using the above tricks you will find the particle movements and sticking part of the code takes seconds rather than minutes per frame. The main slowdown is now in the display code.

Jason.

Diffusion-Limited Aggregation

Posted by softologyblog on August 29, 2016

Diffusion-limited aggregation creates branched and coral like structures by the process of randomly moving particles that touch and stick to existing stationary particles.

All of the images and movies in this post were created with Visions of Chaos.

Real Life Experiments

If you put an electrodeposition cell into a copper sulfate solution you can get results like the following images.

2D Diffusion-limited Aggregation

DLA is a simple process to simulate in the computer and was one of my first simulations that I ever coded. For the simplest example we can consider a 2D scenario that follows the following rules;

1. Take a grid of pixels and clear all pixels to white.
2. Make the center pixel black.
3. Pick a random edge point on any of the 4 edges.
4. Create a particle at that edge point.
5. Move the particle randomly 1 pixel in any of the 8 directions (N,S,E,W,NE,NW,SE,SW). This is the “diffusion”.
6. If the particle goes off the screen kill it and go to step 4 to create a new particle.
7. If the particle moves next to the center pixel it gets stuck to it and stays there. This is the “aggregation”. A new particle is then started.
Repeat this process as long as necessary (usually until the DLA structure grows enough to touch the edge of the screen).

When I asked some of my “non-nerd” aquaintances what pattern would result from this they all said a random blob like pattern. In reality though the pattern produced is far from a blob and more of a coral like branched dendritic structure. When you think about it for a minute it does make perfect sense. Because the moving particles are all coming from outside the fixed structure they have less of a chance of randomly walking between branches and getting to the inner parts of the DLA structure.

All of the following sample images can be clicked to see them at full 4K resolution.

Here is an image created by using the steps listed above. Starting from a single centered black pixel, random moving pixels are launched from the edge of the screen and randomly move around until they either stick to the existing structure or move off the screen.

Start configuration: Single centered black pixel
Random pixels launched from: rectangle surrounding existing structure
Neighbours checked for an existing pixel: N, S, E, W, NE, NW, SE, SW
Particles stick condition: when they move next to a single stuck particle

The change in this next example is that neighbouring pixels are only checked in the N, S, E and W directions. This leads to horizonal and vertical shaped branching.

Start configuration: Single centered black pixel
Random pixels launched from: rectangle surrounding existing structure
Neighbours checked for an existing pixel: N, S, E, W
Particles stick condition: when they move next to a single stuck particle

There are many alternate ways to tweak the rules when the DLA simulation is running.

Paul Bourke’s DLA page introduces a “stickiness” probability. For this you select a probability of a particle sticking to the existing DLA structure when it touches it.

Decreasing probability of a particle sticking leads to more clumpy or hairy structures.

Another method is to have a set count of hits before a particle sticks. This gives similar results to using a probability.

Another change to experiment with is having a threshold neighbour count random particles have to have before sticking. For example in this next image all 8 neighbours were checked and only 1 hit was required to stick, but the moving particles needed to have at least 2 fixed neighbour particles before they stuck to the existing structure.

The first 50 hits only need 1 neighbour. This build a small starting structure which all the following hits stick to with 2 or more neighbours.

That gives a more clumpy effect without the extra “hairyness” of just adding more hit counts before sticking.

This seems a happy balance to get thick branches yet not too fuzzy ones.

The next two examples launch particles from the middle of the screen with the screen edges set as stationary particles.

Start configuration: Edges of screen set to black pixels
Random pixels launched from: middle of the screen
Neighbours checked for an existing pixel: N, S, E, W, NE, NW, SE, SW
Particles stick condition: once a moving particle has 1 or more stuck neighbours

These next three use a circle as the target area. Particles are launched from the center of the screen.

Start configuration: Circle of black pixels
Random pixels launched from: middle of the screen
Neighbours checked for an existing pixel: N, S, E, W, NE, NW, SE, SW
Particles stick condition: once a moving particle has 1 or more stuck neighbours

This next image is a vertical 2D DLA. Particles drop from the top of the screen and attach to existing seed particles along the bottom of the screen. Color of sticking particles uses the color of the particle they stick to.

Start configuration: Bottom of screen is fixed particles
Random pixels launched from: top of the screen
Neighbours checked for an existing pixel: S, SE, SW
Particles stick condition: once a moving particle has 1 or more stuck neighbours

Dendron Diffusion-limited Aggregation

Another DLA method is Golan Levin’s Dendron DLA. He kindly provided java source code so I could experiment with Dendron myself. Here are a few sample images.

Hopefully all of the above examples shows the wide variety of 2D DLA possible and the various methods that can produce them. This post was mainly going to be about 3D DLA, but I got carried away trying all the 2D possibilities above.

3D Diffusion-limited Aggregation

DLA can be extended into 3 dimensions. Launch the random particles from a sphere rather than a surroundiong circle. Check for a hit against the 27 possible neighbours for each 3D grid cell.

For these movies I used default software based OpenGL spheres. Nothing fancy. Slow, but still managable with some overnight renders.

In this first sample movie particles stuck once they had 6 neighbours. In the end their are approximately 4 million total spheres making up the DLA structure.

This second example needed 25 hits before a particle stuck and a particle needed 5 neighbours to be considered stuck. This results in a much more dense coral like structure.

Note: see here for my latest much improved 3D DLA results.

A Quick Note About Ambient Occlusion

Ambient occlusion is when areas inside nooks and crannies are shaded darker because light would have more trouble reaching them. Normally to get accurate ambient occlusion you raytrace a hemisphere of rays from the surface point seeing how many objects the rays intersect. The more hits, the darker the shading. This is a slow process. For the previous 3D DLA movies I cheated and used a method of counting how many neighbour particles the current sphere has. The more neighbours the darker the sphere was shaded. This gives a good enough fake AO.

Programming Tip

A speedup some people do not realise is when launching random particles. Use a circle or rectangle just slightly larger than the current DLA structure. No need to start random points far from the structure.

Other Diffusion-limited Aggregation Links

For many years now the ultimate inspiration in DLA for me has been Andy Lomas.

http://www.andylomas.com/aggregationImages.html

His images like this next one are very nice.

Another change Andy uses is to launch the random walker particles in patterns that influence the structure shape as in this next image.

Future Changes

1. More particles. The above 2 movies have between 4 and 5 million particle spheres at the end of the movies. Even more particles would give more natural looking structures like the Andy Lomas examples.

2. Better rendering. Using software (non-GPU) OpenGL works but it is slow. Getting a real ray traced result supporting real ambient occlusion and global illumination would be more impressive.

3. Controlled launching of particles to create different structure shapes other than a growing sphere.

Jason.

Softology's Blog

Fractals, Cellular Automata, Chaos Theory, Machine Learning, Science, Space, etc

Category Archives: Diffusion-limited Aggregation

Pushing 3D Diffusion-Limited Aggregation even further

Diffusion-Limited Aggregation