Inspiration for this post
The other day I saw this YouTube video of a Belousov-Zhabotinsky Cellular Automaton (BZ CA) by John BitSavage
After a while of running in an oscillating state it begins to grow cell like structures. I had never seen this in BZ CAs before. I have seen similar cell like growths in Digital Inkblot CAs and in the Yin Yang Fire CA. Seeing John’s results different to the usual BZ CA was what got me back into researching BZ in more depth.
The Belousov-Zhabotinsky Reaction
Belousov-Zhabotinsky Reactions (see here for more info) are examples of a chemical reactions that can oscillate between two different states and form intetesting patterns when performed in shallow petri dishes.
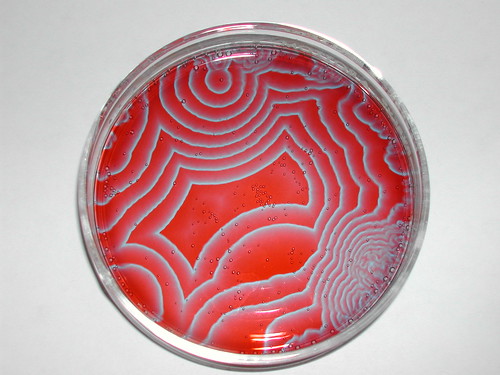
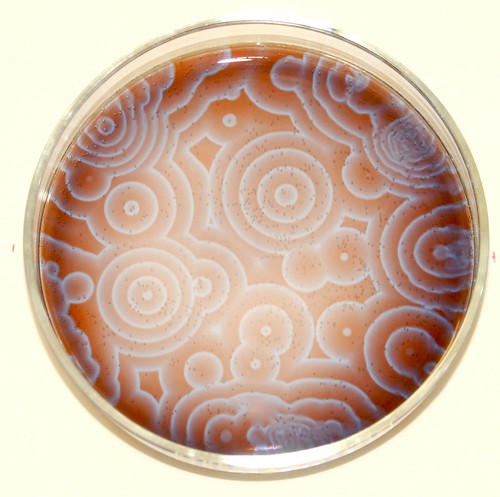
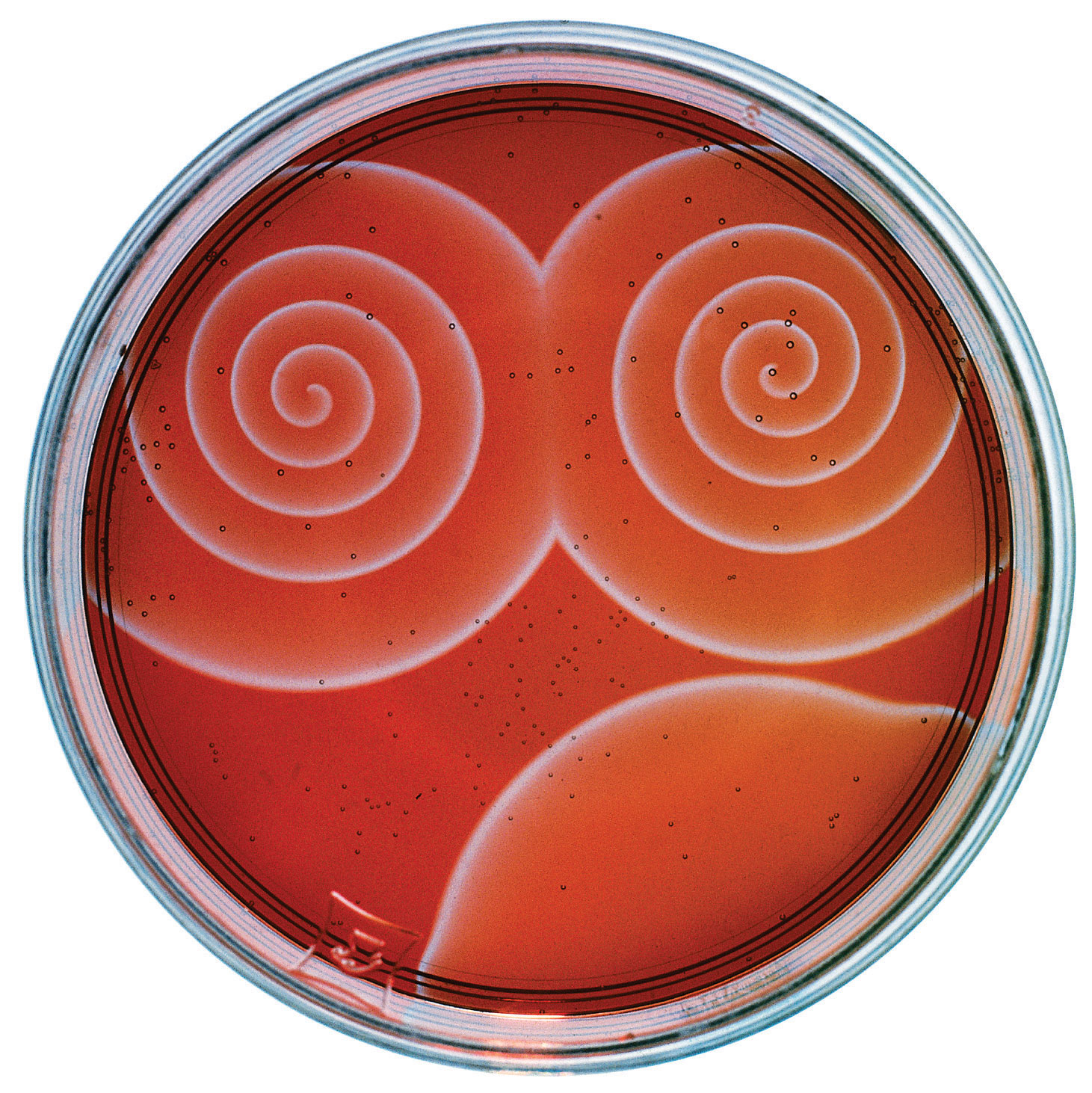
Here are some sample high res images of real BZ reaction by Stephen Morris. Click for full size.
and some other images from around the Internet
and some sample movies I found on YouTube
The Hodgepodge Machine Cellular Automaton
Back in August 1988, Scientific American‘s Computer Recreations section had an article by A. K. Dewdney named “The hodgepodge machine makes waves”. After a fair bit of hunting around I could not find any copies of the article online so I ended up paying $8 USD to get the issue in PDF format. The PDF is a high quality version of the issue, but $8 is still a rip off.
In the article Dewdney describes the “hodgepodge machine” cellular automaton designed by Martin Gerhardt and Heike Schuster of the University of Bielefeld in West Germany. A copy of their original paper can be seen here.
How the Hodgepodge Machine works
The inidividual cells/pixels in the hodgepodge automaton have n+1 states (between 0 and n). Cells at state 0 are considered “healthy” and cells at the maximum state n are said to be “ill”. All cells with states inbetween 0 and n are “infected” with the larger the state representing the greater level of infection.
Each cycle of the cellular automaton a series of rules are applied to each cell depending on its state.
(a) If the cell is healthy (i.e., in state 0) then its new state is [a/k1] + [b/k2], where a is the number of infected cells among its eight neighbors, b is the number of ill cells among its neighbors, and k1 and k2 are constants. Here “[]” means the integer part of the number enclosed, so that, for example, [7/3] = [2+1/3] = 2.
(b) If the cell is ill (i.e., in state n) then it miraculously becomes healthy (i.e., its state becomes 0).
(c) If the cell is infected (i.e., in a state other than 0 and n) then its new state is [s/(a+b+1)] + g, where a and b are as above, s is the sum of the states of the cell and of its neighbors and g is a constant.
The parameters given for these CA are usual q (for max states), k1 and k2 (the above constants) and g (which is a constant for how quickly the infection tends to spread).
My previous limited history experimenting with BZ
Years ago I implemented BZ CA in Visions of Chaos (I have now correctly renamed the mode Hodgepodge Machine) and got the following result. This resolution used to be considered the norm for YouTube and looked OK on lower resolution screens. How times have changed.
The above run used these parameters
q=200
k1=3
k2=3
g=28
Replicating Gerhardt and Miner’s results
Gerhadt and Miner used fixed values of k1=2 and k2=3. The majority of their experiments used a grid size of q=20 (ie only 20×20 cells) without a wraparound toroidal world. This leaves the single infection spreading g variable to play with. Their paper states they used values of g between 1 and 10, but I get no spirals with g in that range.
Here are a few samples which are 512×512 sized grids with wraparound edges and many thousands of generations to be sure they had finally settled down. Each cell is 2×2 pixels in size so they are 1024×1024 images.
q=100, k1=2, k2=3, g=5
q=100, k1=2, k2=3, g=20
q=100, k1=2, k2=3, g=25
q=100, k1=2, k2=3, g=30
Results from other parameters
q=100, k1=3, k2=3, g=10
q=100, k1=3, k2=3, g=15
q=100, k1=3, k2=3, g=20
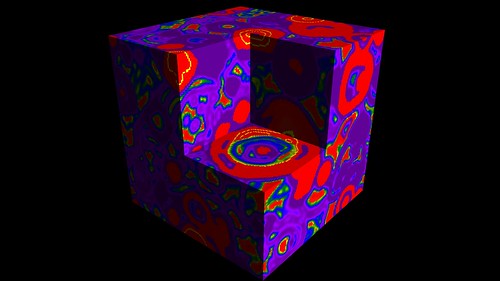
Extending into 3D
The next logical step was extending it into three dimensions. This blog post from Rudy Rucker shows a 3D BZ CA from Harry Fu back in 2004 for his Master’s degree writing project. I must be a nerd as I whipped up my 3D version over two afternoons. Surprisingly there are no other references to experiments with 3D Hodgepodge that I can find.
The algorithms are almost identical to their 2D counterparts. The Moore neighborhood is extended into three dimensions (so 26 neighbors rather than 8 in the 2D version). It is difficult to see the internal structures as they are hidden from view. Methods I have used to try and see more of the internals are to slice out 1/8th of the cubes and to render only some of the states.
Clicking these sample images will show them in 4K resolution.
q=100, k1=1, k2=18, g=43 (150x150x150 grid)
q=100, k1=1, k2=18, g=43 (150x150x150 grid – same as previous with a 1/8th slice out to see the same patterns are extending through the 3D structure)
q=100, k1=1, k2=18, g=43 (150x150x150 grid – same rules again, but this time with only state 0 to state 50 cells being shown)
q=100, k1=2, k2=3, g=15 (150x150x150 grid)
q=100, k1=3, k2=6, g=31 (150x150x150 grid)
q=100, k1=4, k2=6, g=10 (150x150x150 grid)
q=100, k1=4, k2=6, g=10 (150x150x150 grid – same rules as the previous image – without the 1/8th slice – with only states 70 to 100 visible)
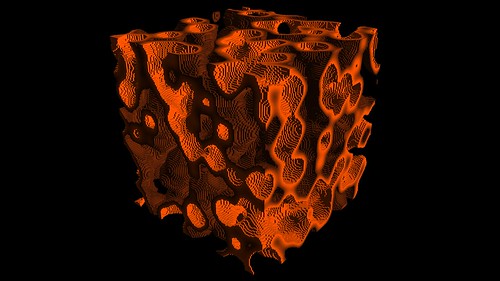
q=100, k1=3, k2=31, g=43 (250x250x250 sized grid – 15,625,000 total cells)
q=100, k1=4, k2=12, g=34 (350x350x350 sized grid – 42,875,000 total cells)
q=100, k1=1, k2=9, g=36 (400x400x400 sized grid – 64,000,000 total cells)
Download Visions of Chaos if you would like to experiment with both 2D and 3D Hodgepodge Machine cellular automata. If you find any interesting rules please let know in the comments or via email.



















Pingback: Hodgepodge Cellular Automaton – daily.hip
Hi,
first time I saw the BZ automata was precisely in that Scientific American in 1988 I still have the magazine somewhere at home.
In that time I implemented it on my Sinclair QL in pure 68K ASM, I was using a LUT for a/k1 and b/k2 and s/a it was quick enough to get decent animation speed, IIRC I THINK I was using a 128×128 matrix.
Recently I re-implemented it in Vulkan using Shader language ( GLSL SpirV variant ) as a “debug test” for some stuff I am implementing.
Weird thing I found, if you “normalize” everything in a [0..1] range and you transform all computations into floating point .. .. I could NOT find any parameters set ( yet ) to make it work.
To make it work I had to “rescale” it all into 0..q and compute “as you do” , I also found out that if you perform those division again in FP without truncation to integer – i.e. let’s say instead of using floor ( a/k1) you use ( a/k1) – you don’t get same results, you don’t get the “swirling curling” stuff but some odd stuff.
I found out the choices of parameters are really critical, there always seems to be “a critical point for g” where finally some cyclical behaviour happens, otherwise it will always quickly stabilize to a steady state.
In my experiment also I use the “toroidal wrap around” cords and a “Moore” (3×3) neighbour.
Also initially I was randomly filling up all the texture ( 512 x 512 ) with random numbers between 0 and q, I found out that in many cases that was leading to some immediate stability but to get “the swirl pattern” it’s better to start with a matrix that has at least some “border” of cells all 0, I use a border of 64 cells in my 512×512 and I fill up all the rest with random values.
I’d love to try a 3D variant as well .. but this means I’ll have to re-implement also my “voxel renderer” unless I go “cheap” and I cheat trying to render some millions of cubes 😀
But yes I always loved this automata, it’s pretty 🙂