4D Cellular Automata

Inspiration

I was inspired to try 4D Cellular Automata after seeing david196609876‘s YouTube 4D CA movies like this one;

After having some previous success with 3D cellular automata I had to have a go at implementing 4D Cellular Automata in Visions of Chaos.

A quick note of rule notation format

CA rules are usually specified in the survival/birth/states format. Conway’s original Game of Life is 23/2/2, so cells with 2 or 3 neighbors survive, empty spots with 2 neighbors become alive, and there are 2 states per cell (on or off).

If the rule starts with a / then it means there are no neighbor survival rules. eg /5/10 means no living cells survive no matter how many neighbor cells they have, a cell will be born at an empty location if it has exactly 5 neighbors, and each cell has 10 possible states it can be in.

I use the same format for the rules shown in this post. Because there can be rule numbers with 2 digits they need to separated with commas. Ranges of numbers can be separated with a hyphen. eg a rule may be (just made up to show as an example) 1-3,5,15/3,7,12-25/10.

Coding a 4D CA

Extending the 3D CA world to 4D is simple enough from a programming perspective. You just add the 4th dimension (usually denoted by the letter w) to your arrays. Rather than ca[x,y,z] you now have ca[x,y,z,w].

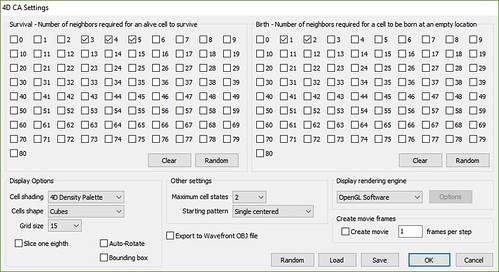
The number of possible neighbors for each cell grows from 26 (3^3-1) neighbors in 3D to 80 (3^4-1) in 4D. This means the settings dialog now needs 162 check boxes so the user can specify the parameters for birth and survival.

Counting the current neighbors of each cell now involves looping through the extra dimension, so again rather than just and X, Y and Z loop, you now add an additional W loop to count the 4 dimensional neighbors in the ca[x,y,z,w] array. This slows the processing down by an order of magnitude so larger grids are much slower to process. For example a 10x10x10 3D array has 10x10x10x26=26,000 neighbor count checks. A 4D 10x10x10x10 array has 10x10x10x10x80=800,000 cells to check while counting neighbors of each cell. Pushing the grid size to 100 gets the check count code up to 100x100x100x100x80=8,000,000,000 checks. The loops that do the neighbor checking/counting are the main slowdown when generating 4D CA. Since first writing this post I have now added parallel multiple CPU support for the 4D CA mode so it will use all of the available CPU cores for greater speeds.

Displaying 4D in 3D space

Now comes the tricky part. How do you display a 4 dimensional array in 3D?

To be able to truly show the 4 dimensions of (for example) a 10x10x10x10 sized 4D CA you would need to show 10 3D grids of 10x10x10 cells. I wanted some way to show 4 dimensions in the available 3 dimensions.

The first method I tried was to display a cell if any of the W dimension cells were active. This is the basic algorithm

for loopx=1 to gridsize do
    for loopy=1 to gridsize do
        for loopz=1 to gridsize do
        begin
             showcell=false
             for loopw=1 to gridsize do
             if ca[loopx,loopy,loopz,loopw]>0 then showcell=true
             if showcell=true then DisplayCellIn3DAtXYZ
        end

Another method is to pick a fixed W value. This is like slicing the 4th dimension into 3 for plotting. When I tested this method I found because you are relying on just one of the W dimension cells to tell you to plot or not to plot the 3D cell many/most of the resulting frames can be blank. The above method of “if any w dimension cells are on then plot it” works better for a consistent display every frame.

One other method to try is having a threshold value for the w dimension. Keep this low or the 3D cell will not trigger as active and won’t be rendered. So the above code would change to

for loopx=1 to gridsize do
    for loopy=1 to gridsize do
        for loopz=1 to gridsize do
        begin
             showcell=false
             cellcount=0
             for loopw=1 to gridsize do
             if ca[loopx,loopy,loopz,loopw]>0 then inc(cellcount)
             if cellcount>threshold then showcell=true
             if showcell=true then DisplayCellIn3DAtXYZ
        end

Playing with the threshold gives other insights into the 4th dimension structures of the CA.

Coloring the cells

At this point you have a 3D array containing a bunch of cells to render in 3D space.

These are the methods I currently use to color the cells;

1. RGB cube. Convert the XYZ location into scaled RGB values.

“David 3” /1-3/2

2. White only. Keep all the cells white. Looks good with a nice ambient occlusion renderer like Mitsuba. Also multiple colored lights can work well here too.

“David 2” /1-5/2

3. Color palette. Index into a color palette based on distance of cell from origin.

“Sphere Growth” /5/10

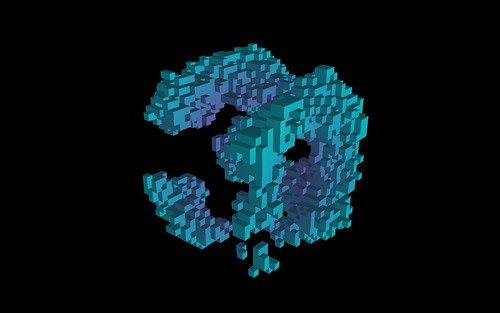
4. Color palette based on the 4th dimension density. For this method you count how many times the current XYZ cell is turned “on” in the W dimension array. Use count/gridsize*255 as an entry into a 256 color palette. This can show other structures/patterns the other methods do not.

“David 1” 3-5/1-2/2

Initial starting patterns

Try a single centered active cell, a block of 3x3x3x3 (remember this is 4D so all 4 dimensions need to be set on) active cells, a 10x10x10x10 block or active (or randomly active) cells, or the full grid filled with random cells.

Rendering engines

Visions of Chaos supports rendering the cell grids using software OpenGL, Mitsuba Renderer and/or Pixar’s RenderMan. OpenGL is good for quick test renders, but for best quality Mitsuba and RenderMan are the better options. Mitsuba performs excellently with even millions of cubes and I tend to use it the most when rendering movies.

“Jason 01” /7,16,20,68/2 – Rendered with OpenGL

“Random Box 01” /1/2 – Rendered with Mitsuba Renderer’s default SunSky setup

“Plaid Box” /1/5 – Rendered with Pixar’s RenderMan

OBJ export

The cell grids can also be exported as Wavefront OBJ files (with material MTL files for coloring) and then imported into other 3D programs like Blender, Cinema4D, Maya, etc.

OBJ export rendered with Blender

OBJ export rendered with Blender – Strange alien satellite discovered near the Orion Nebula – Can you tell I am a Blender amateur?

Results

Here is a quick 4K resolution movie showing some 4D CA rules. For determining active cells in the 3D display I used the first method I mentioned above (if any w dimension cell is active then the XYZ location is plotted).

Help me

I am really interested in hearing any other methods for converting 4D into 3D for display that anyone has come up with. If you have a method that could give a better output than my results in this post let me know.

Also, if you know of any interesting 4D CA rules, or download Visions of Chaos and find any new rules, let me know. Finding interesting rules in 4D space seems much more difficult than in 2D and 3D (and 3D has not been easy). Finding those sweet spots between all cells dying and the grid filling with constant random noise is the real challenge.

Surprisingly there is very little out there about 4D Cellular Automata that I can find so hopefully this post may inspire others to give 4D CA a go.

Jason.