Indexed Totalistic Cellular Automata

Inspiration

This new form of Cellular Automata (at least they are new to me) came from a Tumblr post from Neil Makes Games (@NKnauth on Twitter). His post refers to @LorenSchmidt on Twitter, but I could not find the original post. There is enough info in Neil’s post to let me implement and experiment with these CAs.

Due to lack of a name and because I made some changes to the implementation I called them “Indexed Totalistic Cellular Automata”. The rule is totalistic in that it uses the total counts of neighbor cells to determine the new cell state, and the state counts act as an index into the rule array.

Define the rule

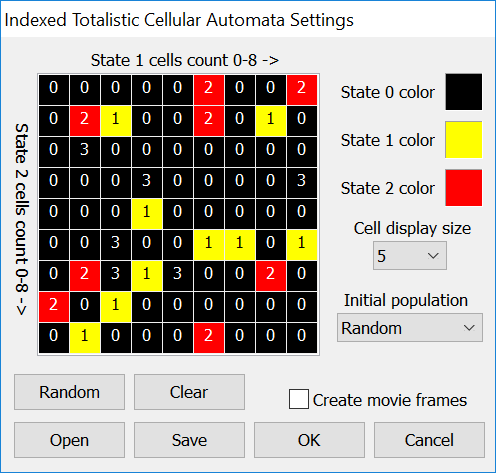
The rule for these CAs are based on a 2D rule table like the following.

The table is mapped to a 9×9 2D rule array of integers. That covers all possible state 1 and state 2 cell counts. There is no “fade out” or “die off” period where cells that “die” go into a semi-dead state before fully dying. All cell updates are based solely on the rule table.

Filling the grid array

The original used values between 1 and 3 to fill the grid. I use between 0 and 3. The different results of including and excluding the 0 are outlined below.

Processing the grid each step

Count the state 1 and state 2 cells in the immediate 8 cell Moore Neighborhood.

Use the state 1 and state 2 counts as an index into the rule array, ie result=rule[state1count,state2count]

If the result is 3 then the cell remains the same. If the result is 1 or 2 then the cell becomes 1 or 2. In the original CA there is no state 0 in the rule array, but I added it in so that if the result is 0 the cell becomes empty.

Results

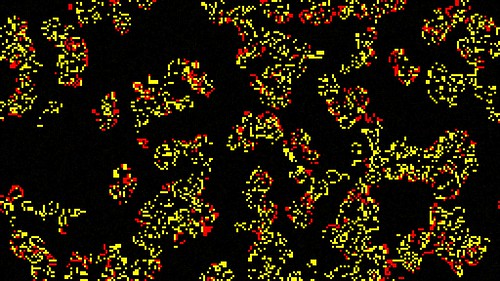
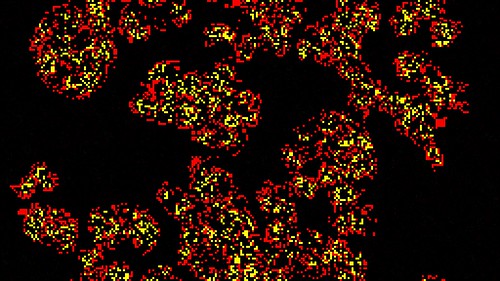
From an initial experiment with these I have seen some interesting results. Click the following images to see an animated gif of the CAs.

There are many unique gliders.

And this fireworks doily like display

Extending the neighborhood size

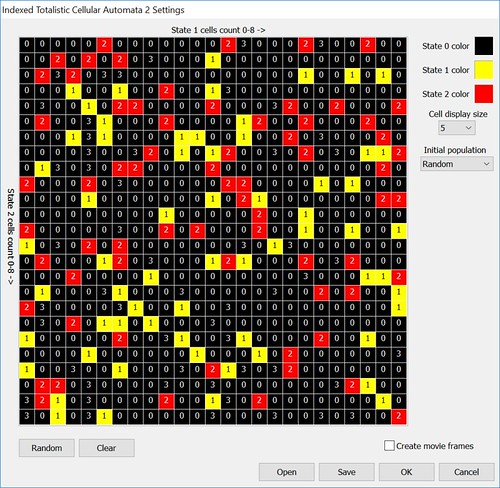
I also played with extending the Moore Neighborhood to all cells within 2 grid distances (total of 24 possible neighbors).

The extended neighborhood tends to give more blobbly amoeba results. Although I have only started to experiment with these CAs so more unique outcomes should hopefully pop up in the future.

Extending to three dimensions

I did some tests with extending into 3D. 26 neighbors per cell. No results worth posting yet. I will update if I find any interesting results in 3D.

Availability

These new CAs are now included with Visions of Chaos. If you do find any new interesting rules, let me know.

Jason.