Inspiration
Erwin Driessens and Maria Verstappen are collaborative Dutch artists that have worked together since 1990 and have created a wide variety of interesting works.
One of their more fascinating projects is Accretor in which they use cellular automata and 3D printing to create physical objects like the following;
They provide some info here which links to this article with more hints of their process but not enough for me to implement the cellular automaton myself. I then emailed Erwin and he was kind enough to clarify the rules he uses. Thanks Erwin.
The rest of this post covers my explanation of and experimentation with the Accretor Cellular Automaton.
Seeding the initial CA array
Start the CA by seeding the middle of an empty 3D grid with a 5x5x5 grid of random cells.
The original Accretor uses 2 or 3 states per cell, but I have been experimenting with up to 5 states per cell. Expanding to more cells is possible and is something to try in the future.
Using a random cell seed allows the resulting structures to grow in more non-uniform ways.
You can also start with a symmetric seed…
…that leads to symmetric results and structures.
The CA rule
The CA rule use a 4 dimensional array of the following dimensions
Rule[0..4,0..6,0..12,0..8]
which corresponds to
[current cell state,face neighbor count,edge neighbor count,corner neighbor count]
Use nested loops to seed the rule array, eg
for stateloop:=0 to (maxstates-1) do
begin
for faceloop:=0 to 6 do
begin
for edgeloop:=0 to 12 do
begin
for cornerloop:=0 to 8 do
begin
if random<0.2 then
rule[stateloop,faceloop,edgeloop,cornerloop]:=random(maxstates)
else
rule[stateloop,faceloop,edgeloop,cornerloop]:=0;
end;
end;
end;
end;
The if random<0.2 above gives a 20% chance of the rule array entry being set. This makes the rule array 1/5th the filled “density”. I found that if the rule array is too dense then the resulting structures tend to be too “blobby” and do not have as interesting resulting structures. I ended up testing various probabilities and in the end now allow the user to configure the fill percentage amount.
Processing the CA
At each step of the CA, empty cells (skip cells that already have an active non state 0 cell) are updated as follows;
1. Count the cell’s neighboring faces, edges and corners.
Rather than count the 26 3D neighbor cells as one group and use that total (as is usually the case with a 3D CA), this method separates the 26 neighbors into 3 groups; faces, edges and corners. See the code below to understand how the faces, edges and corners are counted.
2. If the empty cell does not share at least 1 face with a neighbor stop processing the cell and go onto the next one. A simple if FaceCount<1 then continue check is all that is needed. This ensures the resulting structure is fully connected without cells “joined” at their diagonal corners. It also ensures that the resulting structure can be 3D printed.
3. Use the rule array to update the new cell state (like any CA you use a temp array for the new cell states so all cells are update simultaneously);
4. Repeat as long as necessary. I automatically stop when the CA structure reaches the edge of the 3D array/grid.
Here is some example code that cycles the CA grid each step;
for z:=1 to zcells do
begin
for y:=1 to ycells do
begin
for x:=1 to xcells do
begin
cellstate:=c3d[x,y,z];
t3d[x,y,z]:=cellstate;
//only process empty cells
if cellstate=0 then
begin
//count neighboring cells
FaceCount:=0;
//faces
if c3d[x,y,z-1]>0 then inc(facecount);
if c3d[x,y,z+1]>0 then inc(facecount);
if c3d[x,y-1,z]>0 then inc(facecount);
if c3d[x,y+1,z]>0 then inc(facecount);
if c3d[x+1,y,z]>0 then inc(facecount);
if c3d[x-1,y,z]>0 then inc(facecount);
//must have at least 1 face touching
if facecount>0 then
begin
EdgeCount:=0;
CornerCount:=0;
//edges
if c3d[x,y-1,z-1]>0 then inc(edgecount);
if c3d[x-1,y,z-1]>0 then inc(edgecount);
if c3d[x+1,y,z-1]>0 then inc(edgecount);
if c3d[x,y+1,z-1]>0 then inc(edgecount);
if c3d[x-1,y-1,z]>0 then inc(edgecount);
if c3d[x+1,y-1,z]>0 then inc(edgecount);
if c3d[x-1,y+1,z]>0 then inc(edgecount);
if c3d[x+1,y+1,z]>0 then inc(edgecount);
if c3d[x,y-1,z+1]>0 then inc(edgecount);
if c3d[x-1,y,z+1]>0 then inc(edgecount);
if c3d[x+1,y,z+1]>0 then inc(edgecount);
if c3d[x,y+1,z+1]>0 then inc(edgecount);
//corners
if c3d[x-1,y-1,z-1]>0 then inc(cornercount);
if c3d[x+1,y-1,z-1]>0 then inc(cornercount);
if c3d[x-1,y+1,z-1]>0 then inc(cornercount);
if c3d[x+1,y+1,z-1]>0 then inc(cornercount);
if c3d[x-1,y-1,z+1]>0 then inc(cornercount);
if c3d[x+1,y-1,z+1]>0 then inc(cornercount);
if c3d[x-1,y+1,z+1]>0 then inc(cornercount);
if c3d[x+1,y+1,z+1]>0 then inc(cornercount);
//update temp CA array
t3d[x,y,z]:=rule[cellstate,facecount,edgecount,cornercount];
end;
end;
end;
end;
end;
Number of possible rules
If my maths is right, using a rule with 3 states (0, 1 and 2), 6 faces, 12 edges and 8 corners works out to 3^2457 (2457=3*7*13*9) possible rules. A hugely vast search space to find interesting rules within. 7 rather than 6 for faces because 0 is also a possible face count, so 0,1,2,3,4,5 and 6 are possible face neighbor counts.
That is approximately 1.9 × 10^1172. If the estimated grains of sand on earth is only 7.5 x 10^18 and the atoms in the human body is 7 x 10^27 then that 10^1172 is ridiculously massive.
Searching for interesting rules
Clicking a random rule button multiple times to see if an interesting result occurs gets real boring real fast. Looking for good rules is like the proverbial needle in a haystack, although in this case the haystack is much much larger than your ordinary haystack.
Searching involves looping through multiple random rules looking for possibly interesting results. There a variety of “categories” that results can be classified as when searching;
1. Stagnated. Rules that lead to the initial small seed not growing at all or only growing a few steps then stopping. These are ignored and not saved.
2. Growth with small straight lines from the starting seed. These are classified as “boring”. Once the growth reaches the edge of the grid, it is simple enough to detect these by checking the active cell count vs the grid size and if less than half a percent consider the rule boring.
if cellcount/(gridsize^3)<0.005 then boring
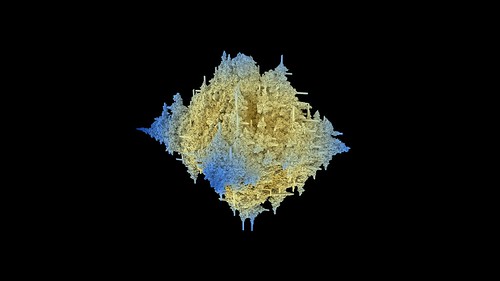
3. Octahedron shapes. A lot of the resulting structures fill an octahedron shaped area. Before the search begins, generate a rule that is known to create an octahedral shape and remember the active cell count. When generating random rules, if the cell count is within +/- 20% the octahedron count then classify it as an octahedron and put it in a separate folder.
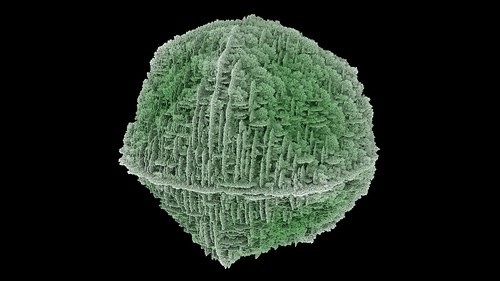
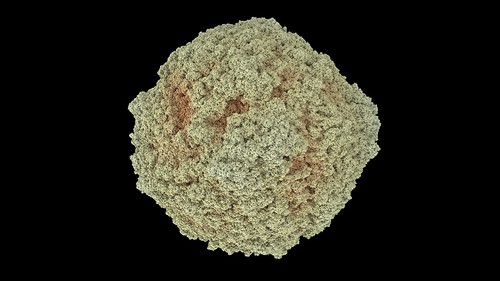
4. Sphere shapes. Another common result. Before the search begins, generate a rule that is known to create a spherical shape and remember the active cell count. When generating random rules, if the cell count is within +/- 20% the sphere count then classify it as an sphere and put it in a separate folder.
5. Slow growth. Erwin has observed that interesting rules tend to be slow growers. A simple way to check for slow growth is to count the steps the CA takes to reach the edge of the grid. If the number of steps is greater than the grid size multiplied by three the rule is considered a slow grower and saved to a separate folder.
6. The rest. If the random rule passes all the above checks then it is considered a possibility. The parameters and a sample image are saved for future checking.
Not all of the above classifiers are bulletproof and 100% reliable, so you will get some incorrectly classified results. Going on active cell count alone is not the most accurate classification method, but it does seem to result in a general weeding out of unwanted results.
After letting the search run for hours or overnight you come back and have a quick scan through the results directories to see if any of the possible good rules are worth further investigation. Once you have a bunch of possible rules that look good they can be rendered at a larger grid size at better quality. I have included the search functionality with Visions of Chaos so you too can hunt for interesting rules if you wish and if you do, let me know if you find any interesting rules.
Display
Use cubes or spheres to render the grid cells. OpenGL is OK for quick test renders, but the lack of proper shadowing and ambient occlusion can make it difficult to see the actual structures.
As has been the case for a while now, I prefer to use the most excellent Mitsuba Renderer. Pixar’s RenderMan is also supported.
The cube grids can also be exported as a WaveFront OBJ file for importing and rendering in other 3D programs like Blender, Maya, Cinema 4D, etc.
Results
Here is a 4K sample movie of the resulting CAs using the methods described in this blog post.
After posting that movie I got numerous complaints about the individual parts ending too quickly. I decided to try rendering longer parts. This can be a real test of patience as once the number of individual cubes rises it can take around half an hour PER FRAME to render. I had 5 PCs churning away 24 hours a day for 2 weeks rendering movies. The result is as follows.
If anyone sees this and complains the parts are still too short they can use their computing resources and generate their own long lasting examples. This has also inspired me to try and develop my own custom raytracer for a lot of cubes or spheres using GPU acceleration. Mitsuba and/or Renderman give really nice shaded results but they both can be very slow when rendering millions of cubes or spheres.
Issues with using a rule array and random numbers
Using a rule array means there cannot be a series of check boxes that the user can check/uncheck to manually set the rule. To make a user settable “rule” I use the random number generator seed value as a rule number. For example setting the rule number to 1234 would set the pseudo-random generator seed to 1234 before filling the rule array with random values. This allows the same steps to be repeatable and the same rules to be run again. It does not however allow me to easily share good rules with others. If for example you coded your own version of the Accretor CA (which I encourage anyone into CA to try) chances are your language’s pseudo-random generator would not use the same code as mine does, so you would get different results to mine. You would get your own unique results but we would not be able to share interesting rules. I have the same issue with my implementation of Voxel Automata Terrain.
Another problem with using a random number generator to seed the array is the limited number of random number sequences that can be generated. In my case the pseudo random generator (a linear congruential generator) takes a seed value that is a 32 bit integer value. This means there can only be a total of 4,294,967,296 possible random rules I can generate and check. 4,294,967,296 may seem like a lot, but it is a tiny fraction of the entire possible rule space and statistically you would think that there are some other interesting rules out there that seeding with a random number generator is going to miss.
Some comments on coding the Accretor CA
Calculate an array that contains each cell’s distance from the center of the grid before starting. This saves costly sqrt calculations during the cycling. I use the distance array for working out what the farthest cell is from the center of the grid which allows a % done stat during generation.
When a new cell becomes active use it’s location to update min/max x,y and z variables. Something like;
maxx:=max(maxx,x+1);
minx:=min(minx,x-1);
maxy:=max(maxy,y+1);
miny:=min(miny,y-1);
maxz:=max(maxz,z+1);
minz:=min(minz,z-1);
Then when cycling the 3D grid each step you only need to loop from zmin to zmax, ymin to ymax, and xmin to xmax. This helps speed things up when the initial growth structure is small. No point looping through the rest of the empty grid when there is no chance of a new cell being born there.
Future Ideas
Extend the neighborhood beyond the immediate 26 neighbor cells. See if more complicated structures appear.
2D Version
See this blog post for some results from experimenting with a 2D version of the Accretor Cellular Automata.
4D Version
I have also extended the Accretor logic into four dimensions. Click the following image to see an example animated GIF file.
No full sample movie yet as I have other things to work on and I don’t have the patience for week long renders at the moment. When I do get some spare time to let my PCs churn I will upload a sample to YouTube and link it here. In the meantime you can play with the 4D version in Visions of Chaos if you are interested as I do include some other samples with it. If you find any other nice examples send them to me.
Availability
Accretor Cellular Automata is now a mode in Visions of Chaos.
Jason.








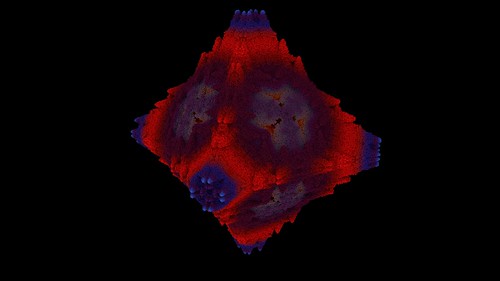








Video thumbnail reminds me of Torbernite, a radioactive mineral. https://periodictable.com/Samples/091.5/s9s.JPG