Origins
This cellular automaton comes from Matthew Guay who describes it in this post on r/cellular_automata on Reddit. There was no name given for these CAs so I have called them “Rule Table Cellular Automata” for my implementation in Visions of Chaos.
The usual behavior for a cellular automata with more than 2 states is that a living (state 1) cell that dies does not become a dead (state 0) cell immediately. Instead the cell goes through a refractory dying period. In a 5 state automata such as this one a state 1 cell that dies would first go through states 2 to 4 each step before finally disappearing and leaving a state 0 empty cell. Using the rule table described below this does not always happen. A cell in a refractory period can suddenly turn back into an alive cell or any other state. This opens up a much wider variety of possible results.
For a 2D example of a rule table based CA I have experimented with in the past see the Indexed Totalistic Cellular Automata.
The Rule Table Explained
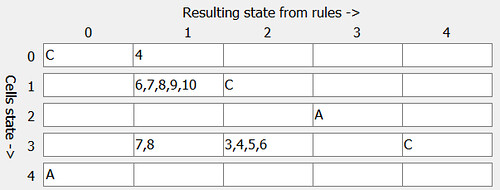
This CA uses a rule table to determine how the cells update. It is a 5 state CA with rules like the following
The current cell state (5 states so cell values are between 0 and 4) is shown down the left hand side. Depending on how many state 1 neighbor cells the current cell has determines the new state value.
For example, for that rule table, if a cell has a state of 3 and has 5 neighbor cells that are state 1, then the next state for the cell will be 2. Take the 4th row down for state 3, then go across until you find count 5, then use that column value for the new cell state.
Matthew also uses C and A characters.
“C” means “all states not already shown in this row”. For the 0 state row only count 4 is specified. The C in count 0 column means any cell that does not have 4 neighbor cells becomes state 0.
“A” means all possible count values. So with the above table, any cell that is in state 4 becomes state 0.
To make it easier, compare the above rule table to a state lookup arrays as follows. This is basically what I construct internally for the CA to use as the CA runs. After playing with the rules a while having the GUI interface be a grid as follows would be much easier to use and easier to understand at a glance. Maybe the idea of using C and A to reduce complexity of displaying the rules makes it more complicated to read? Anyway, I do show the rule table as above to match the original.
State 0 [0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0]
State 1 [2,2,2,2,2,2,1,1,1,1,1,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2]
State 2 [3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3]
State 3 [4,4,4,2,2,2,2,1,1,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4]
State 4 [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0]
That shows the 27 possible results (0 to 26 neighbors) for each cell state. Count a cell’s 26 neighbors and use that count as an index to the new state.
Results
As with all new CA rules the first challenge is finding some good examples within the usual vast search space. Seeing as I have not found a way to detect interesting rules looking for new rules comes down to repeatedly trying random rules hoping for a visually pleasing result. After experimenting with so many CA types over the years I am used to this random process by now. Put a movie on to watch as I repeatedly try random setups. Save the ones that show potential and then manually tweak them to see if anything really interesting happens.
Here is a compilation of interesting rules I found so far.
Availability
If you want to experiment with these CAs yourself they are now included with Visions of Chaos.
Jason.